A slope of line calculator is a useful tool in mathematics for determining the steepness of a line on a graph. By inputting the coordinates of two points on the line, the calculator swiftly computes the slope, which represents the ratio of vertical change (rise) to horizontal change (run) between the points. Utilizing a factoring calculator tool enhances the efficiency of this process, especially when dealing with complex equations or polynomials. Factoring involves breaking down an expression into simpler components, facilitating easier manipulation and calculation. By integrating the factoring calculator tool, users can streamline the process of determining the slope of a line by quickly simplifying any given equations or expressions involved. This amalgamation of tools empowers learners and professionals alike to tackle slope-related problems with ease and precision, fostering a deeper understanding of mathematical concepts and their practical applications.

What Is The Formula For Calculating The Slope Of A Line?

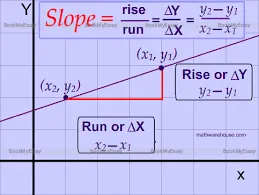
The slope of a line measures its steepness or inclination. The formula to calculate slope, often denoted as "m," is derived from the change in y-coordinates (vertical change) divided by the change in x-coordinates (horizontal change) between two points on the line. Mathematically, it is expressed as:

m=x2​−x1​y2​−y1​​

Where:

• (x1​,y1​) and(x2​,y2​) are any two points on the line.

To ease calculations, using a "Finding Slope Calculator" is efficient. These online tools prompt users to input the coordinates of two points on the line and instantly provide the slope value. This automation reduces errors and saves time, making it particularly useful for students, professionals, and anyone dealing with linear equations or graphs.

How Does The Slope Of A Line Affect Its Steepness?

Understanding the slope of a line is crucial in grasping its steepness. In geometry, the slope represents the ratio of vertical change to horizontal change between any two distinct points on the line. A line with a steep slope rises or falls sharply over a short horizontal distance, indicating greater steepness. Conversely, a line with a gentle slope ascends or descends gradually over a longer horizontal span, implying lesser steepness. The slope's magnitude determines the degree of inclination of the line. When seeking assistance with comprehending these concepts, students often turn to assignment help online. Professional tutors proficient in mathematics elucidate the intricacies of slope and its implications on line steepness, offering tailored explanations and exercises. Through such assistance, learners gain clarity, enabling them to navigate geometric problems with confidence and precision, ultimately enhancing their understanding of slope and its role in determining a line's steepness.

Can You Determine The Slope Of A Line From Two Given Points?

Determining the slope of a line from two given points is crucial in various mathematical applications. By utilizing the formula (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) represent the coordinates of the points, one can easily calculate the slope. However, in complex scenarios involving inverse functions, employing an inverse function calculator becomes indispensable. These calculators provide efficient solutions for finding the slope when the function is not linear or when dealing with functions with inverses. Utilizing an inverse function calculator eliminates manual errors and significantly reduces the time required for computations. Moreover, in fields such as physics, engineering, and economics, where nonlinear relationships are prevalent, the ability to accurately determine slopes using inverse function calculators enhances problem-solving capabilities and facilitates precise analysis of real-world phenomena. Thus, incorporating these calculators into mathematical practice enhances efficiency and accuracy in slope determination, particularly in advanced mathematical contexts.

 What Role Does The Rise And Run Play In Slope Calculation?

Assignment help providers often discuss the significance of rise and run in slope calculation. Rise refers to the vertical change in elevation between two points on a slope, while run signifies the horizontal distance between those points. These elements are crucial as they determine the steepness of the slope. In slope calculation, rise and run are utilized to determine the ratio of vertical change to horizontal distance, known as the slope ratio or gradient. This ratio is commonly expressed as a fraction or a percentage. Understanding the rise and run enables students to comprehend the inclination of a slope, aiding in various disciplines such as mathematics, engineering, and geography. Additionally, rise and run play a fundamental role in construction projects, road design, and land surveying, where accurate slope calculations are essential for safety and efficiency. Hence, mastering the concept of rise and run is paramount for comprehensive slope analysis.

 How Does The BookMyEssay Calculator Handle Different Types Of Lines And Slopes?

The BookMyEssay calculator adeptly handles various types of lines and slopes through its robust algorithmic framework. Whether dealing with horizontal, vertical, diagonal, or curved lines, the calculator employs specialized methods to accurately compute their characteristics. For instance, when encountering horizontal lines with a slope of zero, the calculator swiftly identifies them and provides corresponding results. Similarly, vertical lines, characterized by undefined slopes, are efficiently recognized and processed. Diagonal lines with varying slopes are meticulously analyzed, allowing users to determine their inclinations with precision. Moreover, when faced with curved lines, the calculator employs advanced techniques such as calculus to evaluate slopes at specific points along the curve. Overall, the BookMyEssay calculator's versatility and adaptability enable it to handle a wide array of line types and slopes, empowering users with comprehensive solutions for their mathematical needs.