The roots of cubic equations, involving the form ax³ + bx² + cx + d = 0, can be determined through various methods. Understanding how to solve cubic equations is fundamental in mathematics. The roots may be real or complex, and their determination often involves intricate techniques like Cardano's method, Vieta's formulas, or using the cubic formula derived from these.

To solve cubic equations, several approaches exist, such as factoring, synthetic division, or utilizing the rational root theorem to find potential solutions. When faced with irreducible cubics, mathematicians employ methods involving trigonometric or hyperbolic functions to unearth complex roots.

The intricate nature of cubic equations necessitates a grasp of algebraic manipulation and a variety of problem-solving strategies. Mastery of these methods not only reveals the roots of cubic equations but also enhances mathematical problem-solving skills overall.

What Is The General Form Of A Cubic Equation?

In mathematics, a cubic equation assumes the form ax3+bx2+cx+d=0. To aid in solving or analyzing such equations, seeking "Mathematics Assignment Help" is beneficial. The general form represents a polynomial equation of degree three, where a, 'b', 'c', and 'd' are coefficients. Solving cubics typically involves various methods, including factoring, completing the square, or using the cubic formula. Factoring equations manually can be intricate, making tools like a "factoring equations calculator" invaluable for faster and more accurate results. This form encapsulates the fundamental structure of cubic equations, pivotal in understanding higher-degree polynomials. Through mathematical assistance and leveraging technological aids, comprehending and solving cubic equations becomes more accessible, fostering a deeper understanding of algebraic concepts and problem-solving strategies.

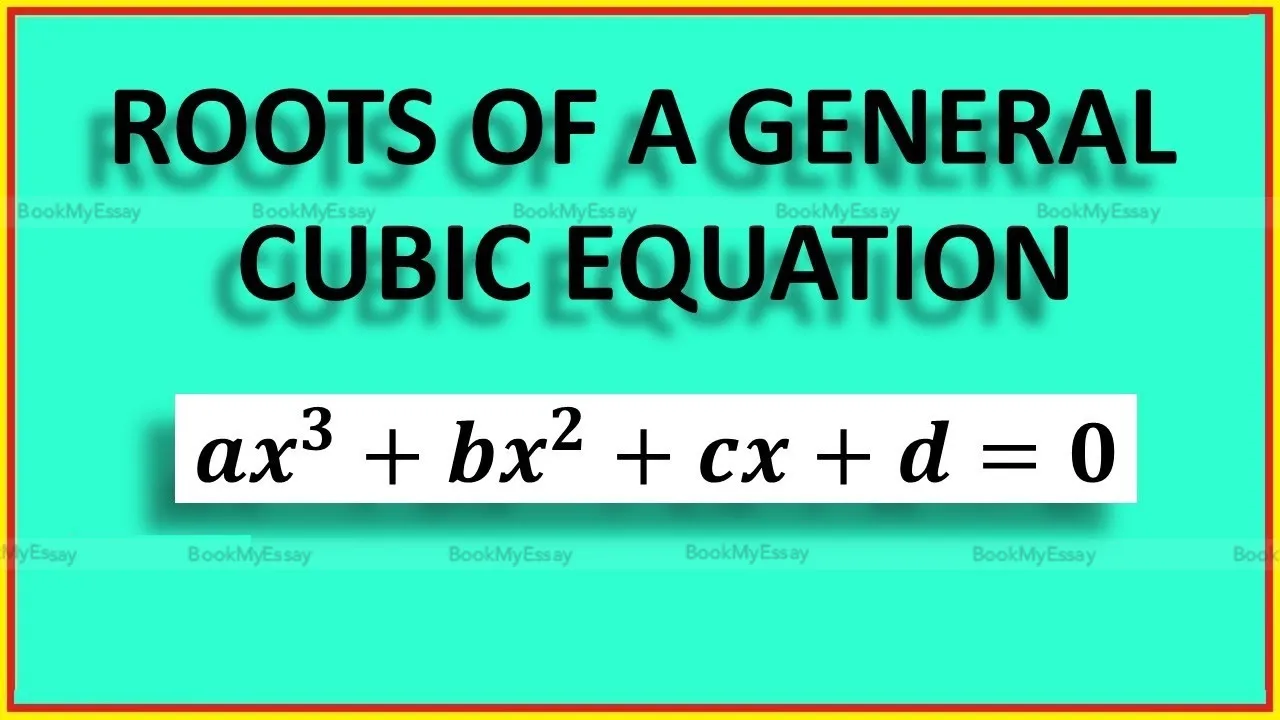
Could You Describe The Cubic Expression Factoring Process?

Understanding the cubic expression factoring process is pivotal in algebraic geometry assignment help. This method involves manipulating cubic equations to their factored form. By employing techniques like grouping or applying formulas like the sum or difference of cubes, one simplifies complex cubic expressions into linear and quadratic factors. The process demands a strong grasp of algebraic principles and factorization methods.

However, when dealing with quadratic equations, solving quadratic equations by factoring a calculator expedites the process. These calculators swiftly factorize quadratic equations, aiding in quick solutions by identifying roots or intercepts accurately. While mastering manual factoring techniques enhances conceptual understanding, utilizing technological tools like solving quadratic equations by factoring calculators expedites problem-solving in practical scenarios, aligning with the needs of modern algebraic geometry assignments.

How Is The Cubic Formula Identified And Used?

The cubic formula, derived from Cardano's method, addresses cubic equations. Its identification involves manipulating coefficients to solve for roots. Its complexity often leads to alternatives like factoring or numerical methods. When seeking help with assignments online, various resources offer step-by-step guides or specialized tools, including solving quadratic equation calculators, aiding in solving cubic equations efficiently. These platforms simplify intricate calculations, guiding users through the process by inputting coefficients and delivering precise solutions. Understanding the cubic formula's application enhances problem-solving skills, essential in mathematical and scientific fields. While the formula's complexity may deter direct use, online assistance and calculators streamline the process, making it more accessible and comprehensible for learners and practitioners alike.

What Parts Do Long Division And Synthetic Division Play In Cubic Solving?

Understanding long division and synthetic division is pivotal in solving cubic equations. Long division systematically breaks down polynomials, enabling the extraction of roots and factors. It's a fundamental technique that allows precise evaluation of cubic equations. On the other hand, synthetic division is a swift, simplified method specifically for dividing polynomials by linear factors, aiding in identifying roots efficiently. Both methods complement each other, offering different approaches to tackle cubic equations. Mastering these techniques not only enhances problem-solving abilities but also strengthens overall mathematical proficiency. To improve geometry skills, practicing with equation balancer calculators and seeking assignment help that incorporates these concepts can provide crucial insights and practical applications, reinforcing a deeper understanding of cubic solving within the context of geometric problem-solving.

How Can BookMyEssay Help With Assignments Using Cubic Equations?

BookMyEssay serves as an invaluable resource for assignments involving cubic equations, offering tailored homework writing help. Specializing in academic assistance, it stands out among homework helper websites in Australia. Their expertise in cubic equations aids students in understanding the complex aspects of solving cubic equations. BookMyEssay provides comprehensive guidance through tutorials, explanatory content, and personalized assistance, ensuring a deeper comprehension of cubic formulas and problem-solving techniques. With a team of proficient writers and subject matter experts, they furnish assignment solutions that adhere to academic standards, utilizing methods like equation balancer calculators to enhance learning. BookMyEssay commitment to delivering precise and well-researched content fosters improved skills in geometry, providing important suggestions for mastering cubic equations while elevating students' academic performance.