Matrix reflection is a mathematical concept employed in linear algebra, computer graphics, and various scientific disciplines. A reflection matrix is a transformation matrix that produces a mirror image of a geometric object across a specified plane. In the context of computer graphics, matrix reflection plays a crucial role in creating realistic visual effects. By manipulating reflection matrices, developers can simulate the way light interacts with surfaces, producing lifelike reflections and shadows.

In linear algebra, a reflection matrix is used to represent a reflection transformation. It captures the essence of mirroring an object across a line, plane, or other hyperplanes. This concept extends beyond mathematics, finding applications in physics, engineering, and computer science. Understanding matrix reflection is fundamental for designing algorithms and models that accurately depict real-world phenomena. As technology advances, the importance of matrix reflection becomes increasingly apparent, influencing the development of virtual environments, simulations, and computational simulations that mirror the complexities of the physical world.

Can You Explain The Role Of Matrices In Reflective Transformations?

Matrices play a crucial role in understanding and implementing reflective transformations in the realm of mathematics and computer graphics. When exploring the concept of reflective transformations, matrices serve as powerful tools for expressing geometric changes in a concise and systematic manner. In this context, matrix transformations become integral to the analysis of reflective processes, enabling a comprehensive understanding of how objects and shapes behave under reflection.

For students seeking clarity in this complex subject, Matrix Transformations Assignment Help becomes essential. Expert guidance aids in deciphering the intricacies of matrices, allowing students to master the application of reflective transformations with precision. By leveraging matrices, one can efficiently represent reflection operations, simplifying the mathematical representation of transformations across various dimensions. In summary, matrices facilitate a structured approach to comprehending and applying reflective transformations, and seeking professional assistance through Matrix Transformations Assignment Help ensures a smoother journey for students navigating this intricate domain.

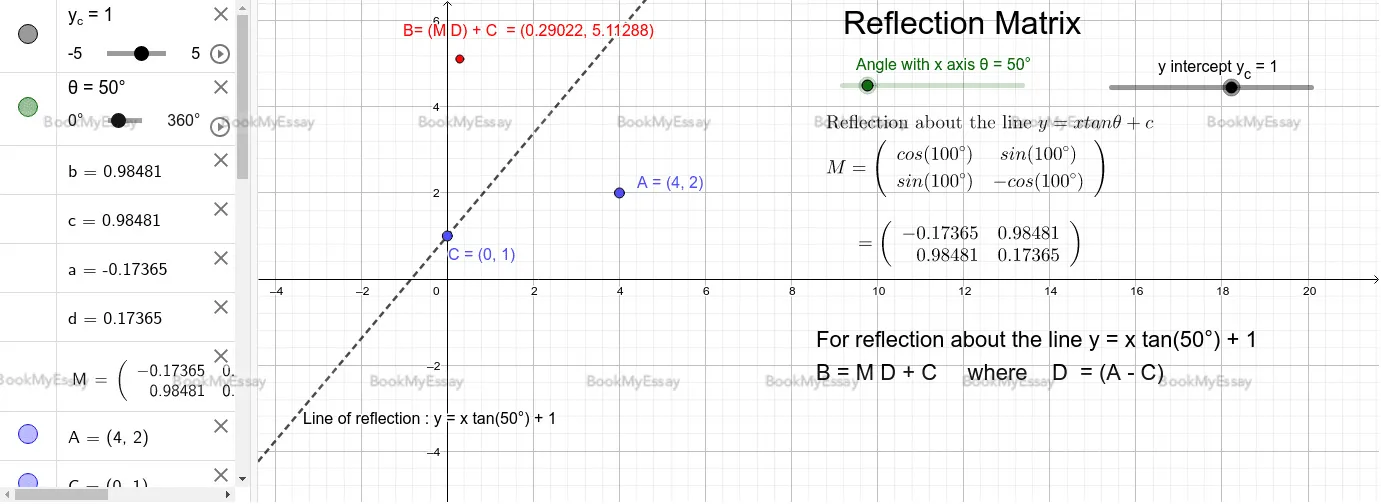
What Are The Key Properties Of A Matrix Reflection In Linear Algebra?

Matrix reflections in linear algebra involve transforming points or vectors across a specified axis or plane. Key properties of matrix reflections include orthogonality and idempotence. An orthogonal matrix, used in the reflection transformation, preserves vector lengths and angles. This ensures that the reflection does not distort the geometry of the objects being transformed. Idempotence is another crucial property, indicating that applying the reflection matrix twice yields the same result as applying it once. In the context of Matrix Method Assignment Help, understanding these properties becomes essential. Assignment Help Online services can guide students in comprehending the intricacies of matrix reflections, helping them apply these concepts to solve problems effectively. Through these services, students can grasp the fundamental principles of linear algebra, ensuring a solid foundation for further exploration of advanced topics in mathematics and related fields. Overall, a comprehensive understanding of the key properties of matrix reflections is vital for mastering linear algebra concepts.

What Is The Significance Of Eigenvalues In The Context Of Matrix Reflection?

In the realm of Academic Writing Help and Assignment Assistance, particularly in subjects like mathematics and linear algebra, understanding the significance of eigenvalues becomes crucial, especially in the context of matrix reflection. Eigenvalues play a pivotal role in analyzing transformations, such as reflections, which are fundamental in various academic disciplines. In the vibrant academic environment of Perth, where students seek reliable Assignment Help in mastering complex topics, comprehending eigenvalues becomes a key to unlocking the mysteries of matrix reflections.

Eigenvalues reveal essential information about the transformation properties of matrices, offering insights into how they stretch, compress, or, in the case of reflections, invert space. Students availing Assignment Help in Perth can benefit from grasping the significance of eigenvalues in matrix reflection as it facilitates a deeper understanding of geometric transformations, paving the way for more insightful and accurate analyses. In essence, eigenvalues become a guiding light for students navigating the intricate landscapes of matrix transformations, ensuring a solid foundation for academic success.

How Can BookMyEssay Help With Reflection on the Matrix?

BookMyEssay serves as a comprehensive Assignment Help Service, offering invaluable assistance in unraveling the complexities of reflecting on the Matrix. Navigating through the intricacies of this philosophical masterpiece requires a deep understanding of its themes, symbolism, and underlying concepts. BookMyEssay's experts, well-versed in the nuances of the Matrix, provide tailored guidance to students seeking clarity and insight.

The platform's specialized Matrix reflection support encompasses detailed analysis, critical interpretation, and thought-provoking discussions. Whether dissecting the film's philosophical implications or delving into its technological and societal commentary, BookMyEssay's team ensures a thorough exploration of key themes. Through personalized assistance, students gain a profound understanding of the Matrix's layers, fostering intellectual growth and enhancing their academic prowess.

In addition to facilitating a profound comprehension of the Matrix, BookMyEssay's Assignment Help Service offers practical tools for effective writing, ensuring that reflections are not only insightful but also well-articulated. With BookMyEssay, students embark on a journey of academic excellence, guided by experts committed to elevating their understanding and appreciation of the Matrix.