If you're tackling a math assignment and need to find the volume of a sphere, fret not, as it's not as complicated as it might seem. Here's a simple guide to help you through it:

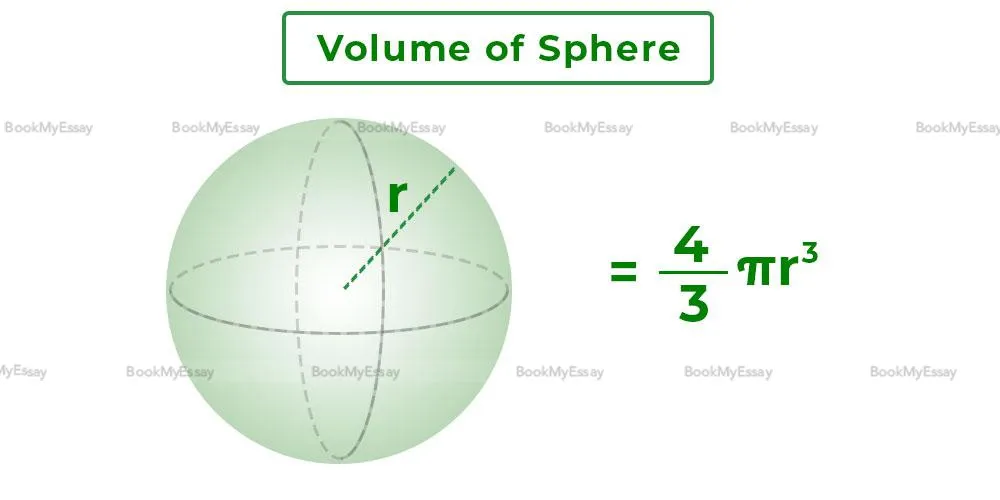
To find the volume of a sphere, you'll need to know its radius (the distance from the center to any point on its surface). The formula for volume is V = (4/3)πr³, where V represents the volume and r stands for the radius.

Here's how to proceed:

1. Begin by identifying the radius of the sphere.
2. Plug the radius value into the formula V = (4/3)πr³.
3. Calculate the cube of the radius (r³).
4. Multiply the result by (4/3)π.
5. This will give you the volume of the sphere in cubic units.

By following these steps, you can easily determine the volume of any sphere, solving your math assignment with confidence. If you encounter any hurdles along the way, don't hesitate to seek further math assignment help.

What Formula Is Used To Calculate The Volume Of A Sphere?

Mathcad Assignment Help and math equation solvers frequently employ the formula for calculating the volume of a sphere. This formula, integral to various mathematical applications, is V = (4/3)πr³. Here, "V" represents the volume of the sphere, "π" denotes the mathematical constant pi (approximately 3.14159), and "r" signifies the radius of the sphere. By cubing the radius and multiplying it by four-thirds and pi, one can efficiently determine the volume. This formula's simplicity belies its profound utility, as it facilitates the computation of volumes across a diverse array of spheres, whether in the realm of geometry, physics, or engineering. Mathcad Assignment Help services and math equation solver often leverage this formula to swiftly solve problems involving spheres, aiding students and professionals alike in their mathematical endeavors. With its elegance and efficacy, the formula for sphere volume stands as a cornerstone of mathematical analysis and problem-solving methodologies.

How Do You Determine The Radius Of A Sphere?

When seeking Assignment Assistance or guidance as an Assignment Provider, determining the radius of a sphere involves straightforward mathematical principles. The radius refers to the distance from the center of the sphere to any point on its surface, and it plays a crucial role in various calculations involving spheres. One common method to find the radius is by using the sphere's volume or surface area formulas. For instance, if provided with the volume of the sphere, you can use the formula V = (4/3)πr³, where V represents the volume and r denotes the radius. Solving for r gives you the radius of the sphere. Similarly, if you have the surface area of the sphere, you can use the formula A = 4πr², where A represents the surface area. By rearranging the formula and solving for r, you can determine the radius. Understanding these formulas and their applications is essential for effective problem-solving in assignments related to spheres.

What Units Are Typically Used When Expressing Sphere Volume?

When delving into the realm of geometry, particularly spheres, the discourse on volume invariably arises. In academic settings, such discussions are common, often becoming focal points in assignments and papers. When pondering the units employed to articulate sphere volume, a few key contenders emerge: cubic units dominate the discourse, with cubic centimeters (cm³) and cubic meters (m³) prevailing. These units seamlessly integrate with the concept of volume, facilitating clear and concise communication of spatial capacity. Additionally, in more specialized contexts, alternative units such as liters (L) or gallons (gal) might surface, especially when considering practical applications. However, in the academic landscape, the focus often rests on the fundamental cubic units for their clarity and universality. Thus, when embarking on assignments or crafting scholarly papers exploring sphere volume, a firm grasp of these units is imperative, ensuring precision and coherence in mathematical discourse. For further elucidation or assistance in navigating such topics, seeking out resources like Assignment Paper Help can provide invaluable support and guidance.

Features Of BookMyEssay

BookMyEssay offers an array of features tailored to simplify math homework. Through intuitive design and user-friendly interfaces, students can navigate effortlessly, making their math assignments more manageable. The platform provides Simple Ways to Make the Math Homework Easy and Simple, employing techniques that break down complex problems into digestible steps.

One notable feature is its comprehensive database of math resources, including tutorials, practice exercises, and explanatory videos. These resources cater to various learning styles, ensuring that every student finds a method that resonates with them. Moreover, BookMyEssay offers personalized assistance through its expert tutors, who are readily available to provide guidance and support whenever needed.

The platform also fosters a collaborative learning environment, allowing students to connect with peers facing similar challenges. Through discussion forums and group study sessions, learners can exchange ideas, clarify doubts, and reinforce their understanding of mathematical concepts.

In essence, BookMyEssay stands out for its commitment to simplifying math homework through innovative features and dedicated support, empowering students to excel in their studies with confidence.