To factor a polynomial efficiently, consider utilizing a trinomial factoring calculator. This powerful tool simplifies complex trinomials by breaking them down into their constituent factors. By entering the polynomial into the calculator, it swiftly identifies the trinomial's prime components, aiding in understanding and solving the equation. This automated process saves time and reduces the likelihood of errors associated with manual factoring. Trinomial factoring calculators are particularly advantageous for handling polynomials with multiple terms, allowing for a streamlined approach to mathematical problem-solving. Incorporating technology like trinomial factoring calculators enhances precision and expedites the resolution of polynomial equations, proving invaluable for students and professionals engaged in algebraic computations.

Can you factor the polynomial x^2 - 4?

To factor the polynomial x^2 - 4, you can use a calculator for factoring polynomials. The given expression can be expressed as the difference of squares, which is a special factoring case. The factored form of x^2 - 4 is (x + 2)(x - 2). Utilizing a calculator for factoring polynomials is particularly handy for complex expressions, as it swiftly identifies and displays the factors. This tool streamlines the process, saving time and ensuring accuracy in polynomial factorization. In this case, recognizing the difference of squares pattern is crucial, and a calculator designed for polynomial factoring efficiently handles such patterns to provide the simplified expression.

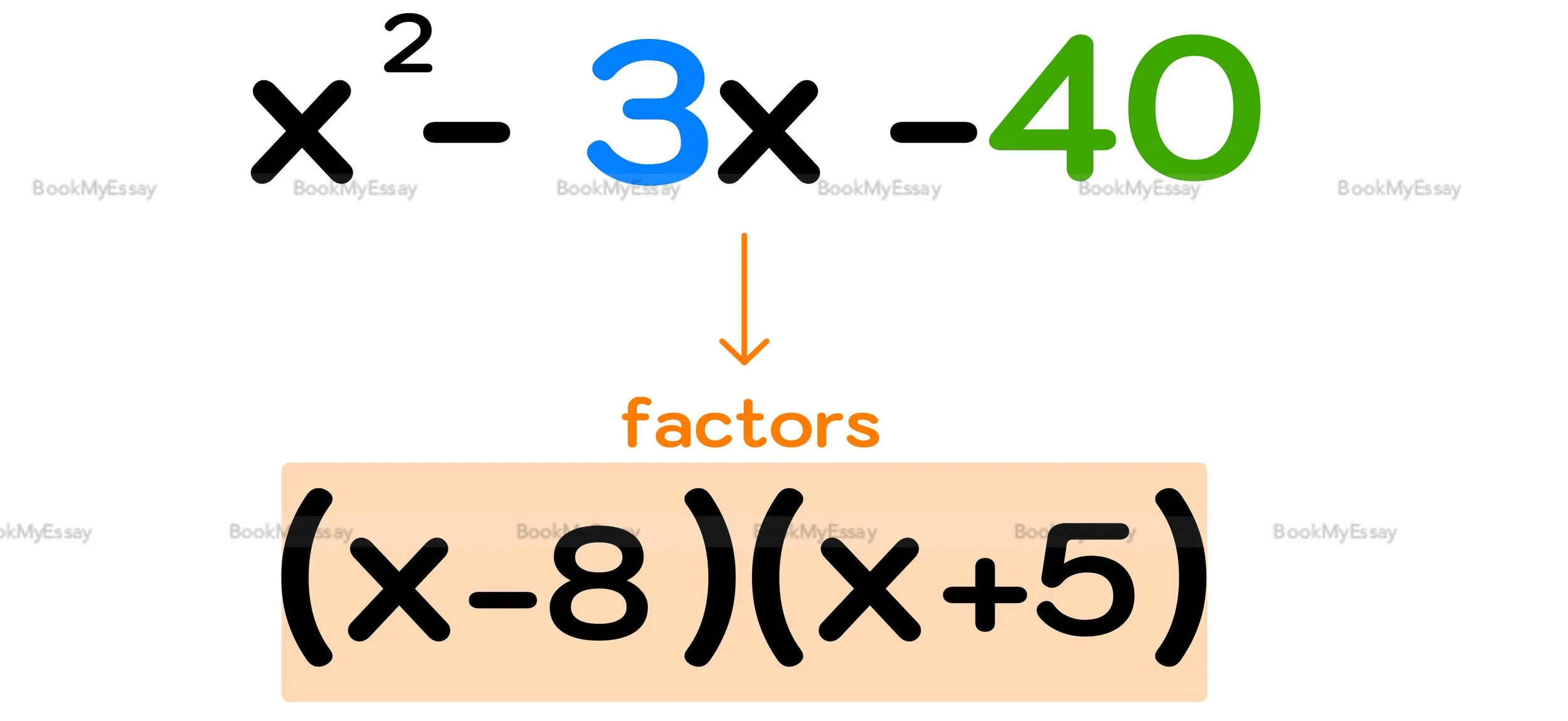
What is the factored form of the polynomial 2x^2 + 6x + 4?

The factored form of the polynomial 2x^2 + 6x + 4 can be determined by factoring out the common factors and expressing it as the product of linear factors. For students seeking assistance, an online assignment writer can provide valuable support in simplifying algebraic expressions and solving polynomial equations. In this case, the factored form of 2x^2 + 6x + 4 is (2x + 2)(x + 2), achieved by factoring out the common factor 2 and recognizing the quadratic trinomial as a perfect square. An online assignment writer can guide students through such mathematical processes, ensuring a comprehensive understanding of factoring techniques and polynomial manipulation for academic success.

How do you factor the quadratic expression 9x^2 - 16?

Factoring polynomials involves breaking down an expression into its constituent factors. For the quadratic expression 9x^2 - 16, valuable facts and points about factoring polynomials come into play. Recognizing it as a difference of squares is crucial; 9x^2 can be expressed as (3x)^2, and 16 as 4^2. Therefore, factoring the expression yields (3x + 4)(3x - 4). This method exploits the algebraic identity a^2 - b^2 = (a + b)(a - b), showcasing its relevance in polynomial factorization. Understanding such techniques is indispensable in algebra, as they form the foundation for solving equations and grasping broader mathematical concepts. Mastery of these principles equips individuals with problem-solving skills applicable in various mathematical scenarios.

Factor the trinomial x^2 + 5x + 6 completely

For students seeking assignment help online, factoring trinomials like x^2 + 5x + 6 is a common challenge. To factorize this expression completely, one must identify two numbers whose sum is the middle coefficient (5) and whose product is the product of the first and last coefficients (1 * 6 = 6). In this case, the numbers are 2 and 3. Therefore, the trinomial factors as (x + 2)(x + 3). Online resources and tutoring services play a crucial role in guiding students through such algebraic problem-solving, offering step-by-step explanations and interactive assistance. Utilizing assignment help online can enhance comprehension, providing valuable insights into factoring techniques and fostering a deeper understanding of mathematical concepts.

How does BookMyEssay approach factoring complex polynomials?

BookMyEssay employs a meticulous approach to factoring complex polynomials, ensuring precision and clarity. The process begins with a comprehensive analysis of the polynomial's structure, identifying common factors and employing appropriate factoring methods. The platform's experts skillfully apply techniques such as grouping, synthetic division, and the use of factor theorem to simplify complex expressions. Emphasizing conceptual understanding, BookMyEssay approach goes beyond mere computation, fostering a deep comprehension of the underlying mathematical principles. Tailoring solutions to individual needs, the platform prioritizes step-by-step explanations, guiding students through the intricacies of factoring complex polynomials. By combining expertise with pedagogical insight, BookMyEssay transforms polynomial factoring into an accessible and enriching learning experience.