The volume of a sphere, a fundamental concept in geometry and calculus, can be derived through a straightforward approach utilizing calculus techniques. At its core lies the integration of infinitesimally thin slices to reconstruct the three-dimensional shape. The formula for the volume of a sphere, \( V = \frac{4}{3} \pi r^3 \), encapsulates this relationship succinctly.

To derive this formula, one can consider a sphere as a collection of infinitely thin disks stacked together. Each disk, when rotated around the sphere's axis, forms a cylindrical shell. By integrating the volumes of these shells from the sphere's center to its surface, one effectively sums the volumes of all infinitesimal slices, culminating in the volume of the entire sphere.

Through calculus, the volume element of a thin disk can be expressed as \( dV = \pi y^2 dx \), where \( y \) represents the radius of the disk at a given position along the axis. By integrating this expression over the range of \( x \) from 0 to the sphere's radius \( r \), one obtains the formula \( V = \frac{4}{3} \pi r^3 \).

Thus, the formula for volume of sphere emerges from the integration of infinitesimal volumes, showcasing the elegant marriage of geometry and calculus in mathematical exploration.

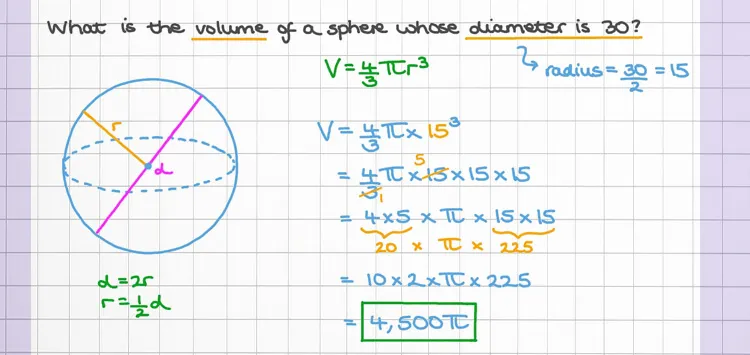
What is the formula for figuring out a sphere's volume?

The formula for calculating the volume of a sphere is a fundamental concept in geometry and mathematics. It provides a precise method to determine the amount of space enclosed within a spherical object. Derived from the ancient Greeks' geometric insights, the formula is remarkably elegant yet powerful in its application. Mathematically, the formula is expressed as V = (4/3)πr^3, where V represents the volume of the sphere and r denotes its radius.

Understanding this formula enables individuals to solve various real-world problems involving spheres, ranging from calculating the capacity of a spherical container to determining the volume of planets or celestial bodies.

For those seeking to comprehend or utilize this formula, there are abundant resources available, including textbooks, online tutorials, and mathematical software. One such resource is the free Math Problem Solver, a tool designed to assist students and professionals in solving mathematical problems efficiently. With the aid of such tools, individuals can input the necessary parameters, such as the radius of the sphere, and quickly obtain the volume without the need for complex manual calculations.

In essence, the formula for the volume of a sphere serves as a cornerstone of geometry and mathematics, offering a precise method to quantify space and enabling practical applications across various fields.

What is the relationship between a sphere's radius and volume?

Understanding the relationship between a sphere's radius and its volume is fundamental in various fields, often explored through coursework writing services and aided by professional experts. The volume of a sphere, a three-dimensional object, is intricately linked to its radius. In mathematical terms, the volume \( V \) of a sphere can be expressed as \( \frac{4}{3} \pi r^3 \), where \( r \) represents the sphere's radius and \( \pi \) is a constant approximately equal to 3.14159.

As the radius of a sphere increases, its volume grows exponentially. This relationship is cubic, meaning that if the radius doubles, the volume increases by a factor of eight. Conversely, if the radius decreases, the volume decreases accordingly. Such a relationship has significant implications in various disciplines, including physics, engineering, and mathematics.

In physics, for instance, understanding the volume-radius relationship of spheres is crucial in calculating properties such as mass, density, and gravitational force. Engineers utilize this relationship when designing structures like pressure vessels or designing efficient packing configurations. Furthermore, mathematicians explore the relationship between a sphere's radius and volume as part of their theoretical investigations into geometric shapes and their properties.

In coursework writing services, professional experts often elucidate this relationship, providing insights into its mathematical underpinnings and practical applications across diverse fields. Understanding the nuanced connection between a sphere's radius and volume enables professionals to make informed decisions and solve complex problems effectively.

When a sphere is divided into infinitely thin disks, what geometric shape is left behind?

When a sphere is divided into infinitely thin disks, the geometric shape left behind is a frustum of a cone. This concept is fundamental in understanding the volume of a sphere and is often explored in mathematical contexts, including academic assignment.

To visualize this, imagine slicing a sphere with parallel planes. As the thickness of these slices approaches zero, each slice forms a circular disk. These disks, when accumulated from the top to the bottom of the sphere, eventually transform the entire sphere into a series of stacked disks. The resulting shape, when the smaller disk at the top is removed, resembles a cone with its tip truncated. This truncated cone is called a frustum of a cone.

Understanding this geometric transformation is crucial in deriving the formula for the volume of a sphere through methods like calculus. By approximating the volume of the sphere with the sum of the volumes of these infinitesimally thin disks, mathematicians are able to arrive at the formula for the volume of a sphere.

In the context of academic assistance, resources like BookMyEssay offer guidance on such mathematical concepts, providing students with insights into understanding complex topics at affordable rates. Their services can aid students in grasping fundamental concepts like the derivation of the volume of a sphere through the decomposition into thin disks, ensuring clarity and comprehension in their studies.