"Corresponding Angles Example Assignment Help" provides crucial assistance to students grappling with the concept of corresponding angles in geometry. Corresponding angles are pairs of angles that occupy the same relative positions at the intersection of a transversal and two parallel lines. Understanding corresponding angles is fundamental in geometry as they enable the exploration of parallel lines and their properties.

This assignment help resource offers practical examples illustrating corresponding angles in various geometric scenarios. By showcasing real-world applications, students can grasp the relevance and utility of corresponding angles beyond abstract theory. Through detailed explanations and step-by-step solutions, students gain clarity on identifying, measuring, and manipulating corresponding angles.

Moreover, this resource aids students in honing their problem-solving skills by presenting diverse exercises and problems involving corresponding angles. By tackling these assignments with assistance, students enhance their geometric reasoning and analytical abilities.

Furthermore, the assistance provided extends beyond mere problem-solving. It encompasses conceptual understanding, fostering a deeper comprehension of the principles underlying corresponding angles. Through tailored guidance and support, students develop confidence in handling complex geometric concepts, laying a solid foundation for further exploration in geometry and related fields. In essence, "Corresponding Angles Example Assignment Help" empowers students to master this fundamental geometric concept effectively.

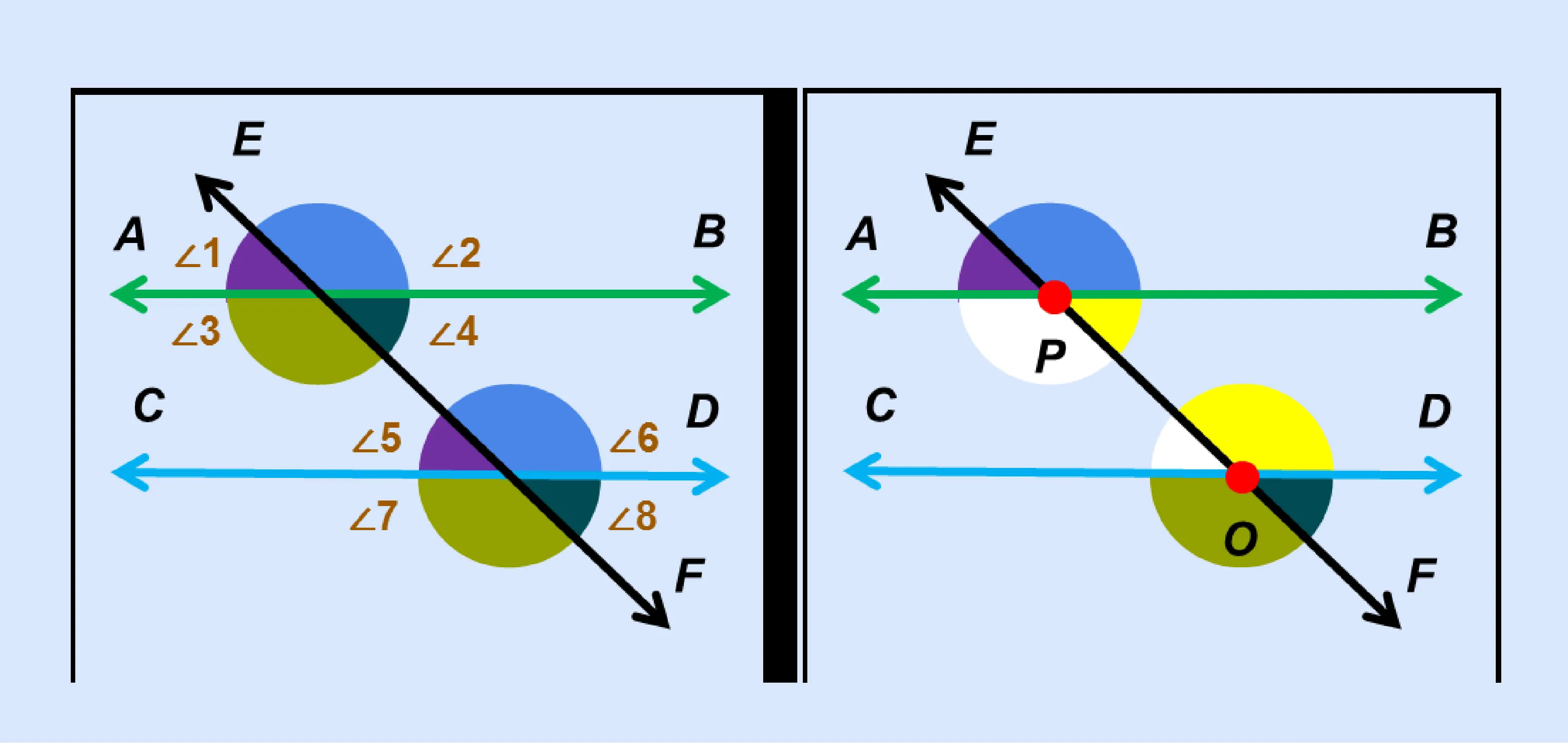
In geometry, what are comparable angles?

In geometry, comparable angles are angles that have the same relative position in relation to the given geometric figures or configurations. They are fundamental elements in understanding the properties of geometric shapes and solving mathematical problems related to angles and lines. Comparable angles occur when two lines are intersected by a transversal, creating a set of angles that have similar positions or orientations.

Comparable angles share certain characteristics with corresponding angles, which are formed when a transversal intersects two parallel lines. However, the distinction lies in the type of lines involved; comparable angles can be found in various geometric configurations, not just limited to parallel lines.

Understanding comparable angles is crucial in mathematical problem-solving, particularly in geometry. By identifying and analyzing these angles, mathematicians and students can deduce various properties of shapes, lines, and configurations. This knowledge aids in proving geometric theorems, constructing geometric proofs, and solving complex mathematical equations.

Furthermore, the comprehension of comparable angles extends beyond theoretical concepts; it has practical applications in fields such as architecture, engineering, and physics. Whether designing structures or analyzing spatial relationships, a solid grasp of comparable angles is indispensable. For students seeking assistance with math assignment help, grasping the concept of comparable angles lays a strong foundation for tackling geometry problems with confidence and accuracy.

In what way do transversals and parallel lines connect to corresponding angles?

Transversals and parallel lines intersect in a manner that unlocks a fundamental concept in geometry: corresponding angles. When a transversal intersects two parallel lines, it creates various angle relationships, with corresponding angles being one of the most significant. Corresponding angles refer to pairs of angles that occupy the same relative positions at the intersection, one on each side of the transversal. These angles are equal in measure when the lines cut by the transversal are parallel. Understanding the connection between transversals, parallel lines, and corresponding angles is crucial for any student seeking assistance with their geometry coursework from an assignment expert.

In coursework, students often encounter problems where they must identify and manipulate corresponding angles to solve geometric puzzles or prove theorems. Mastery of this concept enables students to confidently navigate through tasks involving parallel lines and transversals, making it a cornerstone of geometric problem-solving. Moreover, proficiency in corresponding angles empowers students to construct logical arguments and proofs, showcasing their understanding of geometric principles. Therefore, seeking guidance from an assignment expert to clarify concepts related to corresponding angles ensures students can effectively tackle their coursework, confidently saying, "Do my coursework," while understanding the intricate connections between transversals, parallel lines, and corresponding angles.

Could you give an instance of similar angles in a practical setting?

In practical settings, instances of similar angles can often be found in architectural and engineering designs. Consider a scenario where a construction project requires the installation of a series of streetlights along a straight road. The angles formed between each streetlight and the road can be considered similar. This similarity arises due to the uniform spacing of the streetlights and the parallel nature of the road.

When a team providing Assignment Writing Service, like BookMyEssay, delves into such scenarios, they may analyze the angles to ensure optimal placement of the streetlights for effective illumination and aesthetic appeal. By identifying the similarity between these angles, they can employ geometric principles to calculate measurements such as the height of the poles or the distance between each light, ensuring consistency and coherence in the design.

Furthermore, similar angles in practical settings extend beyond construction projects. They can also be observed in fields like cartography, where mapmakers use similar angles to represent the curvature of the Earth's surface on flat maps accurately. Recognizing and understanding similar angles in such contexts is crucial for professionals providing Assignment Writing Service, as it enables them to apply mathematical concepts to real-world problems effectively.