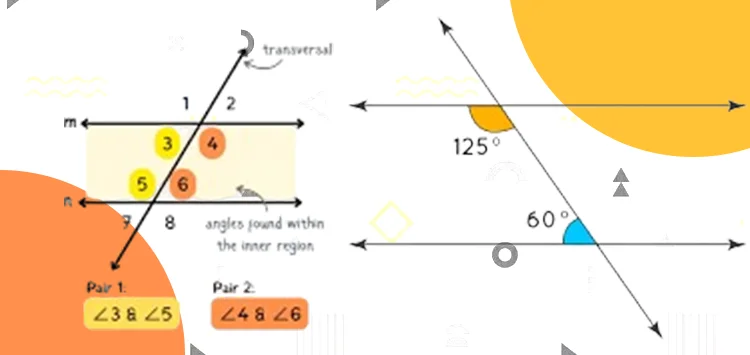
Consecutive interior angles play a crucial role in understanding the relationships between angles in geometric figures, particularly in parallel lines and polygons. When two parallel lines are intersected by a transversal, pairs of consecutive interior angles are formed on the same side of the transversal, but inside the parallel lines. These angles are non-adjacent, sharing a common vertex but lying on different lines.

In the context of polygons, consecutive interior angles refer to the angles formed inside the polygon, sharing a common side but not a common vertex. For example, in a triangle, consecutive interior angles would be angles within the triangle but not adjacent to each other.

Understanding consecutive interior angles is essential for solving various problems related to parallel lines, polygons, and geometric proofs. They follow specific properties, such as being supplementary in the case of parallel lines, meaning that their sum is always equal to 180 degrees.

Students often encounter challenges when dealing with consecutive interior angles, particularly in identifying and utilizing their properties effectively in geometry problems. Seeking interiors assignment help can provide students with the guidance and resources needed to master these concepts, ensuring a solid understanding of geometric principles and enhancing problem-solving skills in the process.

What does a polygon's series of internal angles mean?

A polygon's series of internal angles refers to the measurement of the angles formed within the polygon's interior. This concept is fundamental in geometry and plays a crucial role in understanding the properties and characteristics of polygons. The sum of the internal angles of any polygon can be determined using a formula that depends on the number of sides it has.

For example, in a triangle (a polygon with three sides), the sum of the internal angles is always 180 degrees. Similarly, in a quadrilateral (a polygon with four sides), the sum of the internal angles is always 360 degrees. This pattern continues as the number of sides increases, following a general formula: sum of interior angles = (n - 2) * 180 degrees, where 'n' represents the number of sides of the polygon

Understanding the series of internal angles allows mathematicians and students to solve various problems related to polygons, such as finding missing angles, determining the types of polygons based on their angles, and proving geometric theorems. In practical applications, this knowledge is valuable in fields such as architecture, engineering, and computer graphics.

For students seeking assistance with understanding and solving problems related to polygonal angles, services like "My Assignment Help UK" can provide valuable resources, guidance, and support. Such academic support platforms offer expert assistance, educational materials, and personalized tutoring to help students grasp complex mathematical concepts effectively.

In parallel lines that a transversal cuts, how do successive interior angles behave?

In parallel lines intersected by a transversal, the behavior of successive interior angles is a fundamental concept in geometry, crucial for understanding geometric relationships and proofs. When a transversal cuts parallel lines, it forms eight angles in total, with four pairs of consecutive interior angles.

Successive interior angles are the angles on the same side of the transversal and inside the parallel lines. Crucially, successive interior angles are always congruent. In other words, their measures are equal. This property holds true regardless of the orientation of the parallel lines or the transversal. This geometric principle forms the basis for many proofs and theorems in geometry.

Understanding the behavior of successive interior angles is essential for students tackling geometry problems and proofs, making it a vital topic in the curriculum of any university-level geometry course. Proficiency in this concept allows students to navigate complex geometric structures and formulate logical arguments to prove various theorems.

When students are tasked with a writing assignment for university, exploring topics such as the behavior of successive interior angles in parallel lines intersected by a transversal can provide a rich source of content.

Whether it's explaining the concept, discussing its applications, or demonstrating its significance in geometry, this topic offers ample material for a well-rounded paper. If you're seeking assistance with your paper, don't hesitate to reach out to professional writing services to "Write My Paper For Me," ensuring clarity, coherence, and accuracy in your presentation of this geometric principle.

Is it possible for successive inner angles of a geometric form to be equal? Describe.

In the realm of geometry, the concept of consecutive or successive interior angles holds significant importance, especially in the study of polygons and parallel lines. When it comes to the equality of successive interior angles in a geometric form, it largely depends on the specific shape and configuration of the figure in question.

In many geometric forms, such as triangles and quadrilaterals, it is indeed possible for successive interior angles to be equal. For instance, in an isosceles triangle, where two sides are of equal length, the angles opposite those sides are equal, making them consecutive interior angles. Similarly, in a rectangle or a parallelogram, opposite sides are parallel, and thus their consecutive interior angles are equal.

However, this equality is not a universal rule. In irregular polygons or shapes with varying side lengths and angles, successive interior angles may not be equal. Academic guidance in understanding this concept involves recognizing the properties of different geometric forms and applying relevant theorems and principles to determine the nature of consecutive interior angles.

By providing students with clear explanations, illustrative examples, and problem-solving exercises, academic resources like BookMyEssay play a crucial role in aiding learners to grasp the intricacies of consecutive interior angles and their implications in geometric reasoning and problem-solving.