Quadratic regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a quadratic equation to the data. The quadratic regression equation takes the form y = a + bx + cx^2, where y represents the dependent variable, x represents the independent variable, and a, b, and c are the coefficients that need to be determined through the regression process.

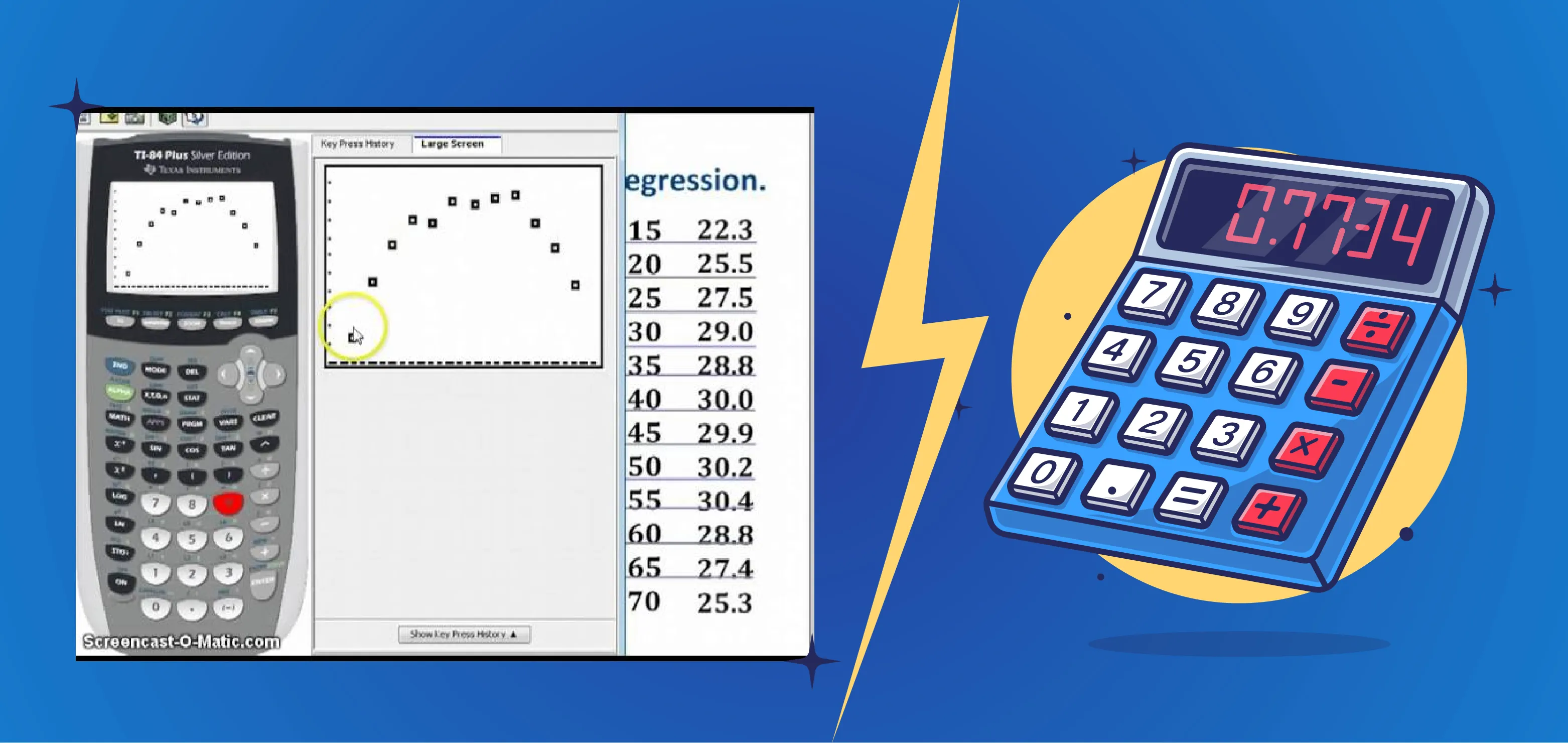
To calculate a quadratic regression, the first step is to collect data points for the variables of interest. Then, using statistical software or mathematical techniques, such as least squares regression, the coefficients a, b, and c are estimated to minimize the sum of the squared differences between the observed and predicted values of the dependent variable. This process involves solving a system of equations or using matrix algebra to find the coefficients that best fit the data.

Once the coefficients are determined, they can be used to construct the quadratic regression equation, which describes the relationship between the variables. This equation allows for the prediction of the dependent variable for any given value of the independent variable within the range of the data. Additionally, assessing the goodness-of-fit measures, such as R-squared or adjusted R-squared, helps to evaluate how well the quadratic regression model fits the data and captures the underlying relationship between the variables. Quadratic regression is particularly useful when the relationship between the variables is curvilinear, and it provides insights into the nature of this non-linear relationship.

Which are the essential steps in the computation of a quadratic regression?

The computation of a quadratic regression involves several essential steps to accurately model the relationship between variables. First, the data must be collected and organized into a dataset with at least three variables: the independent variable (usually denoted as 'x'), the dependent variable ('y'), and a quadratic term ('x^2'). The next step is to calculate the sum of 'x', 'y', 'x^2', 'xy', and the number of observations ('n'). These sums are essential for calculating the coefficients of the quadratic regression equation.

The coefficients of the quadratic regression equation, typically denoted as 'a', 'b', and 'c', are determined using formulas derived from the least squares method. These formulas involve matrix manipulation and solving a system of linear equations. Once the coefficients are calculated, they can be used to construct the quadratic regression equation: Å· = ax^2 + bx + c.

To ensure accuracy and reliability, it's crucial to assess the goodness-of-fit of the quadratic regression model. This involves analyzing metrics such as the coefficient of determination (R^2), which indicates the proportion of the variance in the dependent variable that is predictable from the independent variable(s).

In summary, the essential steps in the computation of a quadratic regression include data collection, calculation of sums, determination of coefficients through matrix manipulation, construction of the regression equation, and evaluation of model fit using statistical metrics. For those seeking assistance, services like "Do My Math Homework" may offer support in navigating these complex calculations and concepts.

How can the coefficients of a quadratic regression model be found?

In solving a quadratic regression model, determining the coefficients involves a series of mathematical steps typically performed using tools such as a math word problem solver. The primary objective is to find the coefficients that best fit the data points onto a quadratic curve. This process usually begins by setting up the regression equation, which comprises terms for the dependent variable, the independent variable, and their respective powers. For instance, in the equation y = ax^2 + bx + c, 'a', 'b', and 'c' are the coefficients to be determined.

The method often employed to find these coefficients is known as least squares regression. This technique minimizes the sum of the squares of the differences between the observed and predicted values. Utilizing calculus, the partial derivatives of this sum are set to zero to find the critical points. Solving these equations yields the values of 'a', 'b', and 'c' that minimize the error, thus providing the coefficients for the quadratic regression model.

Moreover, tools like math word problem solvers streamline this process, offering step-by-step guidance in solving mathematical equations, including quadratic regression problems. By inputting the relevant data and equations, these solvers facilitate swift and accurate determination of the coefficients, making them indispensable aids for students and professionals alike, especially when time is of the essence in completing urgent assignment.

What part does matrix manipulation play in the computation of quadratic regression?

In the realm of statistical analysis and regression modeling, matrix manipulation stands as a fundamental tool, particularly in the computation of quadratic regression. Quadratic regression involves fitting a quadratic function to a set of data points, expressing the relationship between the independent and dependent variables in a polynomial equation of degree two. Matrix manipulation plays a pivotal role in this computation, serving as the backbone of the mathematical operations involved.

BookMyEssay, a renowned assignment provider, elucidates the significance of matrix manipulation in quadratic regression computation. Through their comprehensive guidance, students grasp the intricate process of constructing and solving the system of equations that arise in quadratic regression. These equations, often represented in matrix form, encapsulate the relationships between the predictor variables and the response variable. By leveraging matrix operations such as multiplication, inversion, and decomposition, analysts can efficiently determine the coefficients of the quadratic model, thereby unveiling the underlying patterns within the data.

Furthermore, matrix manipulation facilitates various diagnostic procedures essential for validating the regression model's adequacy. Techniques like matrix factorization aid in assessing multicollinearity among predictors, ensuring the robustness of the regression analysis. BookMyEssay expertise empowers students to navigate through these mathematical intricacies, fostering a deeper understanding of quadratic regression and its applications in real-world scenarios. Through meticulous guidance and exemplary support, they equip learners with the proficiency to excel in statistical analysis and data modeling endeavors.